RUCSAC Problem Solving Strategy: A Guide to Conquer Any Challenge

Problem-solving is a fundamental skill that empowers individuals to overcome obstacles and find effective solutions. When it comes to tackling complex problems, having a structured strategy can greatly enhance your problem-solving abilities.

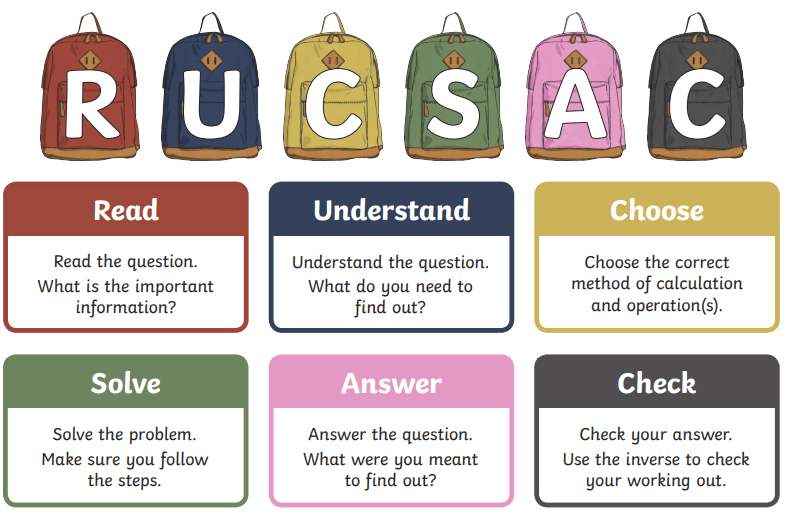
In this blog post, we will explore the RUCSAC problem-solving strategy—an approach widely used in mathematics and beyond. By breaking down problems into manageable steps and considering key factors, the RUCSAC strategy equips you with a roadmap to conquer any challenge.

Here are the steps your students should take to apply the RUCSAC problem-solving method:

We will now apply the RUCSAC problem-solving process in mathematics to approach the maths problem shown in this example.

Step 1: Read and Understand the Problem:

The first step in the RUCSAC problem-solving strategy is to carefully read and understand the problem. Pay attention to the details, identify the main question or task, and underline key information. Ensure you have a clear grasp of what the problem is asking.

Your student must carefully read the question first, picking out any important information that they will need to answer the question. This could include:

The full number of available pizzas (10).
How many of the pizzas Helen and Stephen ate.
That Dexter will be given half of what is left

Step 2: Underline the Relevant Information:

Once you understand the problem, underline or highlight the relevant information. Identify the numbers, quantities, or variables provided in the problem that are necessary to solve it. This step helps you focus on the essential data needed to proceed.

Your student must ensure that they understand what is being asked of them in the question, and what it is that they are trying to find out.

In this case, they are finding out how many pizzas Dexter will be given.

Step 3: Choose a Strategy:

Consider the different problem-solving strategies available to you. RUCSAC is an acronym that stands for Read, Understand, Choose, Solve, Answer, and Check. Evaluate the problem at hand and determine which strategy or combination of strategies is most suitable.

They must thenchoose the calculations that they will make, in order to reach their solution to answer the question.

They will first need to calculate the amount of pizza eaten, then calculate the amount of pizza remaining, and then find out how many of the remaining pizzas Dexter will be given.

Step 4: Solve the Problem:

After choosing a strategy, it’s time to solve the problem. Apply the chosen strategy systematically, following each step. Use the relevant mathematical operations, formulas, or concepts to work through the problem. Show your calculations and work neatly to avoid errors.

They must then solve the question, by accurately performing the correct calculations.

The amount of pizzas eaten totals 3 and 39/40

There are 6 and 1/40 pizzas which remain

Dexter will, therefore, receive half of 6 and 1/40.

Step 5: Answer the Question:

Once you’ve arrived at a numerical solution, answer the main question or task stated in the problem. Write your answer clearly, ensuring it aligns with the context of the problem. Include appropriate units of measurement if necessary.

They will then have their answer.

Half of 6 and 1⁄40 = 3 and 1⁄80

Therefore, Dexter will receive 3 and 1⁄80 pizzas.

Step 6: Check Your Solution:

The final step in the RUCSAC problem-solving strategy is to check your solution. Go back to the problem and reread it, ensuring that your answer makes sense in the given context. Review your calculations to verify their accuracy. If possible, try a different approach or use estimation to confirm the reasonableness of your answer.

At this point, your student mustn’t forget that they should go over and check their working out again. This is so to ensure that they have not made any mistakes along the way.

Conclusion: The RUCSAC problem-solving strategy is a powerful tool that guides you through the problem-solving process step by step. By reading and understanding the problem, underlining relevant information, choosing an appropriate strategy, solving the problem, answering the question, and checking your solution, you can approach any challenge with confidence.

Remember, practice is key to mastering the RUCSAC strategy and problem-solving in general. As you encounter different problems, apply the RUCSAC approach and adapt it to suit your needs. With this strategy in your toolkit, you are equipped to conquer any problem that comes your way, both in mathematics and in various aspects of your life.

The RUCSAC approach to tackling one-step and two-step word problems provides children at key stage 2 children in year 3, year 4, year 5, and year 6,with a systematic means.