Set Theory and Examples

Introductions to Sets

What is a Set?

A set is a collection of items usually of the same kind. The items which belong to a set are called members or elements of the set. We use braces {} to show the members or elements of a set. A set without members or elements is called an empty or null set.

Example 1:

Oma was in math class with her friend Angie. She whispered to Angie that she had just bought a set of winter clothes. The outerwear collection includes a coat, a hat, a scarf, gloves, and boots. Their teacher, Mrs. Nelson, overheard the conversation and asked them:

   What is a set?

Solution:

Luckily for Oma and Angie, their classmate Javay had a math dictionary with him! He quickly looked up the word “set” and defined it for the class as shown below.

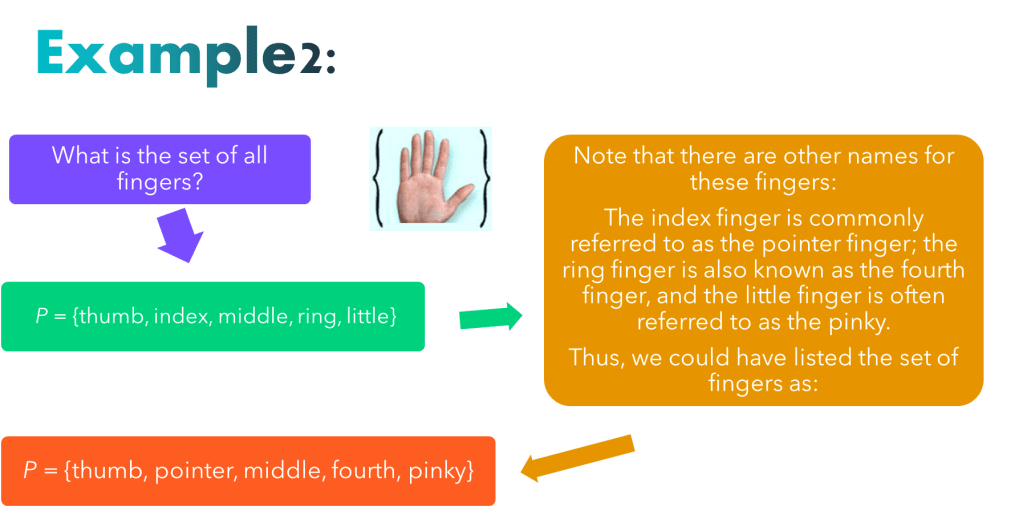
Example 4:

Javay was in art class when the teacher wrote this on the chalkboard: 

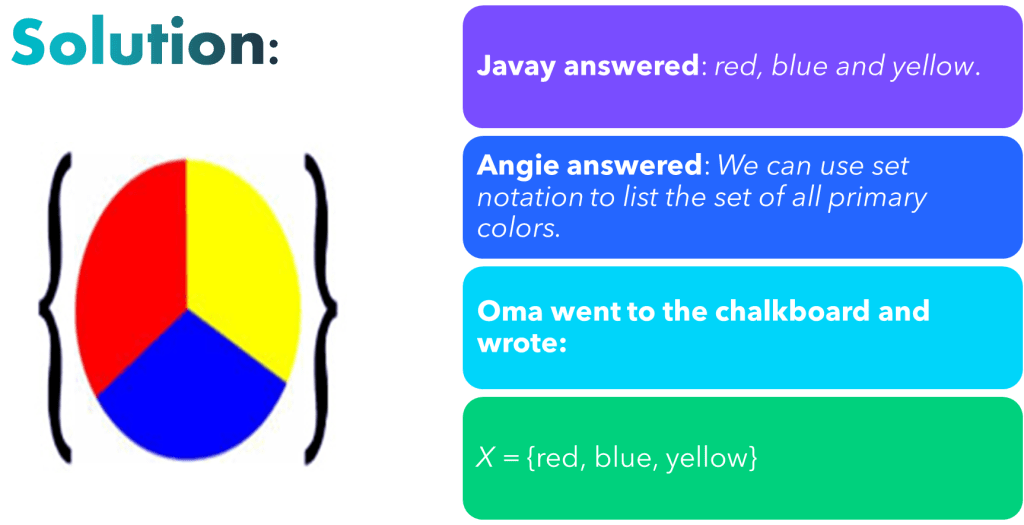
The following conventions are used with sets:

Capital letters are used to denote sets.

Lowercase letters are used to denote elements of sets.

Curly braces { } denote a list of elements in a set.

Example 5: Let R be the set of all vowels in the English alphabet.

Solution: R = {a, e, i, o, u}

---

Example 6: Let G be the set of all whole numbers less than ten.

Solution: G = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

---

Example 7: Let T be the set of all days in a week.

Solution: T = {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}

---

Example 8: Let X be the set of odd numbers less than 12.

Solution: X = {1, 3, 5, 7, 9, 11}

---

Example 9: Let Y be the set of all continents of the world.

Solution: Y = {Asia, Africa, North America, South America, Antarctica, Europe, Australia}

In example 10, set D has 26 elements, so it is easier to describe its elements than to list them.

Similarly, in example 11, set R has 50 elements, so it is easier to describe its elements.

Summary

A set is a collection of objects that have something in common or follow a rule. The objects in the set are called its elements. Curly braces are used to indicate that the objects written between them belong to a set. Every object in a set is unique. It is not necessary to list every object in the set. Instead, the rule that the objects follow can be given in the braces. We can define a set by listing its elements or by describing its elements. The latter method is useful when working with large sets.