Welcome to our mathematics blog! Today, we’re embarking on a journey into the world of set operations, where we’ll explore the concepts of union, intersection, and apply them to different types of sets. By the end of this post, you’ll have a clear understanding of how these operations work and how they relate to finite, infinite, and empty sets. So, let’s dive in!
Understanding Set Operations:
Set operations allow us to combine or compare sets, giving us insights into their relationships and common elements. The two primary set operations we’ll focus on today are union and intersection.
Union of Sets:
The union of two sets, let’s call them Set A and Set B, is the combination of all the unique elements from both sets. In other words, we create a new set that contains all the elements from Set A and Set B without any repetitions. We represent the union operation with the symbol “∪.“

Intersection of Sets:
On the other hand, the intersection of two sets, Set A and Set B, gives us the elements that are common to both sets. It’s the set that contains only the elements that exist in both Set A and Set B. We represent the intersection operation with the symbol “∩.”
Applying Set Operations to Different Types of Sets:
Now, let’s explore how these set operations can be applied to different types of sets, such as finite, infinite, and empty sets.
- Finite Sets: A finite set is a set that has a specific and countable number of elements. When performing set operations on finite sets, we follow the same principles of union and intersection.
For example:
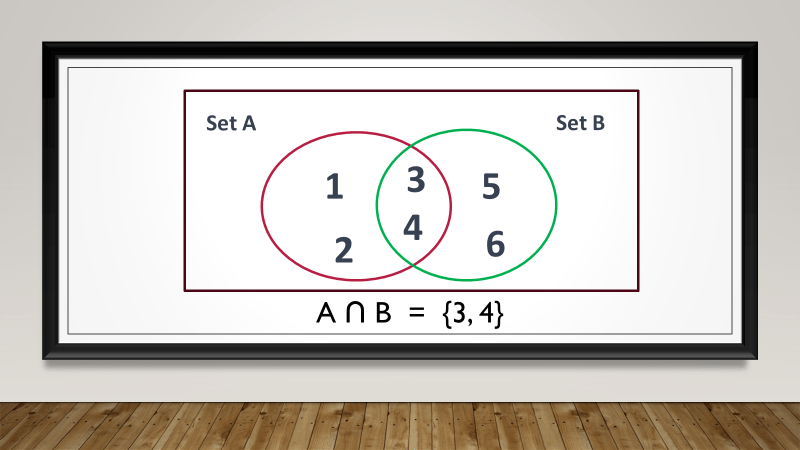
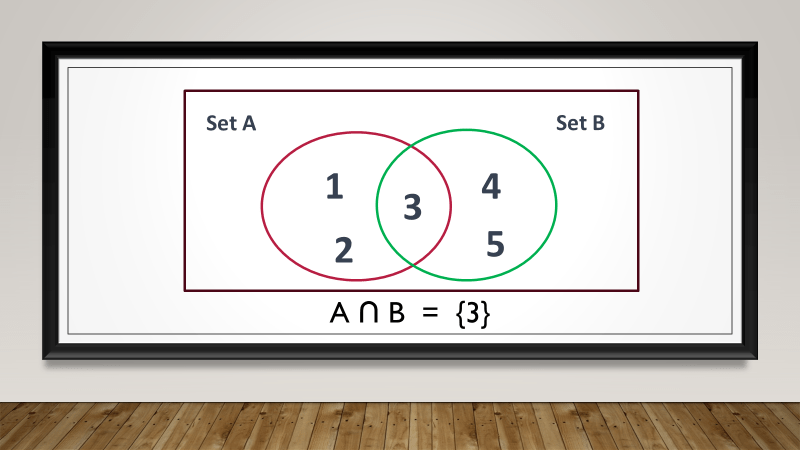
Consider Set A with elements {1, 2, 3} and Set B with elements {3, 4, 5}. The union of Set A and Set B would be {1, 2, 3, 4, 5}, as it combines all the unique elements from both sets.

Similarly, the intersection of Set A and Set B would be {3}, as it only contains the element that is common to both sets.
- Infinite Sets: Infinite sets, as the name suggests, continue indefinitely without an end. When dealing with infinite sets, the union operation remains an infinite set, as it encompasses all the elements from both sets.
For example:
Consider the set of natural numbers {1, 2, 3, 4, …} and the set of even numbers {2, 4, 6, 8, …}. The union of these sets would still be the set of natural numbers because the even numbers are already included within the natural numbers.
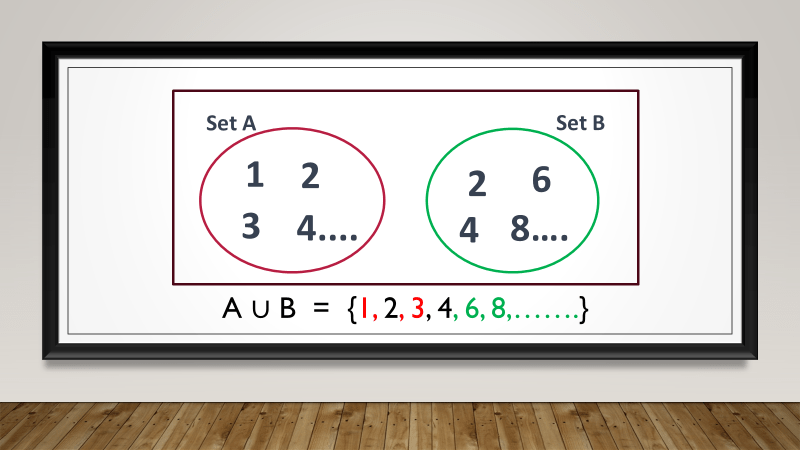
The intersection of infinite sets, however, can result finite or infinite sets, depending on the elements they have in common.

- Empty Sets: An empty set, also known as a null set, contains no elements. When performing set operations involving an empty set, the resulting set will depend on the operation.
For example:
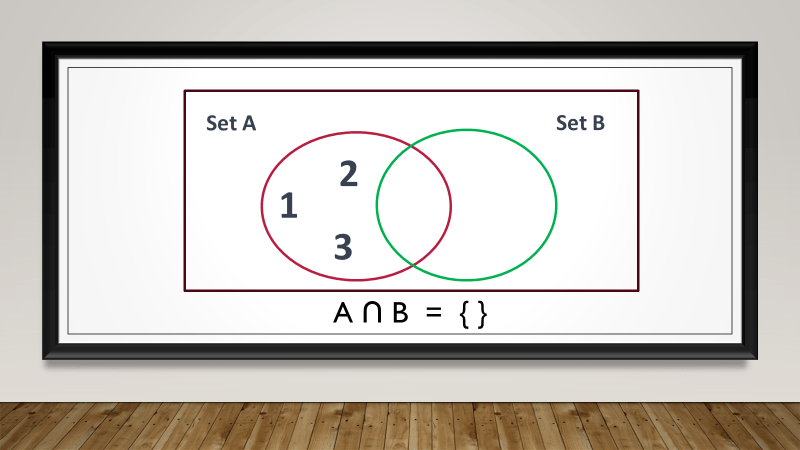
Consider Set A with elements {1, 2, 3} and an empty set, Set B. The union of Set A and Set B would be {1, 2, 3}, as the empty set contributes no elements to the union.

However, the intersection of Set A and Set B would result in an empty set, as there are no common elements between them.
Congratulations! You’ve delved into the world of set operations and applied them to different types of sets. You now understand how union and intersection can be used to combine or find common elements within sets. Remember that these operations can be applied to finite, infinite, and empty sets, each producing distinct results based on their characteristics.



By mastering set operations, you’re equipped with a powerful tool to analyze relationships, find similarities, and explore mathematical concepts further. Keep practicing and applying these operations to enhance your mathematical skills.
We hope this blog post has provided you with a comprehensive understanding of set operations and their applications to various set types. Stay tuned for more exciting mathematical concepts and ideas in our upcoming posts.
Happy exploring and keep embracing the beauty of mathematics!
Related Topics
Understanding Sets: Exploring Finite, Infinite, and Empty Sets
2 thoughts on “Exploring Set Operations: Union, Intersection, and Set Types”